Mastering Logic with Karnaugh Maps: A Comprehensive Guide to 3-Variable Maps

Related Articles: Mastering Logic with Karnaugh Maps: A Comprehensive Guide to 3-Variable Maps

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Mastering Logic with Karnaugh Maps: A Comprehensive Guide to 3-Variable Maps. Let’s weave interesting information and offer fresh perspectives to the readers.

Mastering Logic with Karnaugh Maps: A Comprehensive Guide to 3-Variable Maps

In the realm of digital logic design, simplification is key. The ability to reduce complex Boolean expressions into their most streamlined form translates to efficient hardware implementation, minimizing cost and power consumption. One powerful tool for achieving this simplification is the Karnaugh map, a visual representation of Boolean functions that facilitates the identification of minimal expressions. This guide delves into the intricacies of Karnaugh maps for three variables, providing a comprehensive understanding of their construction, usage, and benefits.

Understanding the Basics: A Visual Representation of Logic

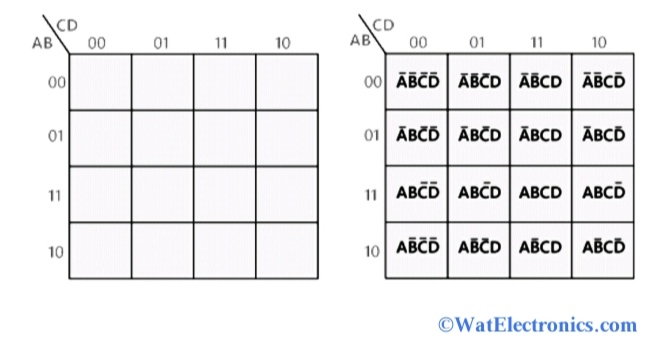
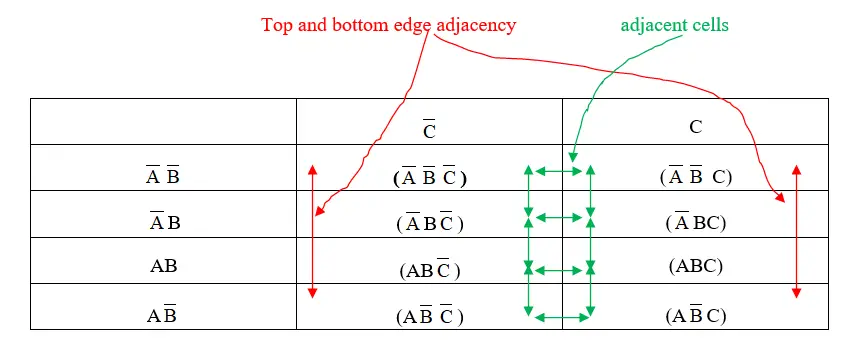
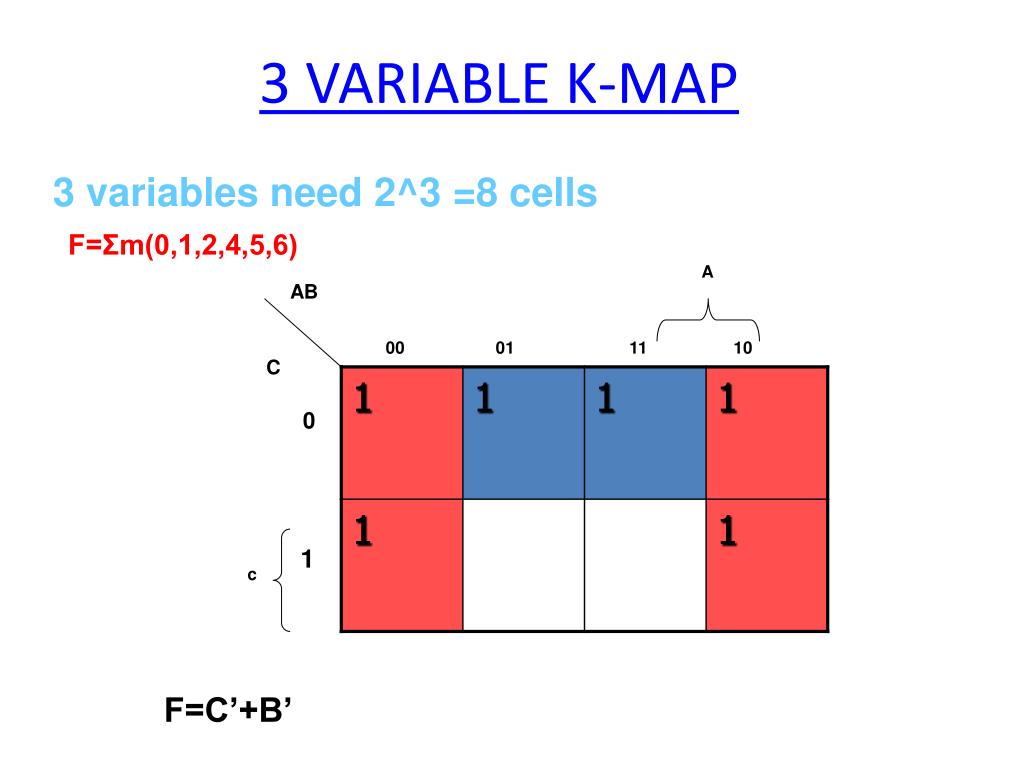
At its core, a Karnaugh map is a graphical tool for representing Boolean functions. It employs a grid structure where each cell corresponds to a unique combination of input variables. The map’s arrangement is carefully designed to exploit the inherent relationships between adjacent cells, allowing for the straightforward identification of logical groupings, known as "implicants."

For a three-variable Karnaugh map, the grid is composed of eight cells, representing all possible combinations of the three input variables. Each variable is assigned a specific column or row, with the order of the variables and their corresponding values determined by the "Gray code" system. This code ensures that adjacent cells differ by only one variable, facilitating the identification of groups.

Constructing a Karnaugh Map for Three Variables: A Step-by-Step Guide

1. Define the Input Variables: Identify the three input variables that define the Boolean function. Label them as A, B, and C for clarity.

2. Determine the Output Values: Establish the output value (0 or 1) for each possible combination of input values. This information can be obtained from a truth table or a verbal description of the function.

3. Create the Grid: Construct a 2×4 grid, with each cell representing a unique combination of the three variables. Label the rows with the values of variables A and B, using Gray code, and the columns with the values of variable C, also using Gray code.

4. Populate the Cells: For each combination of input values, locate the corresponding cell in the map and insert the output value (0 or 1).

Utilizing the Map: Identifying Minimal Expressions

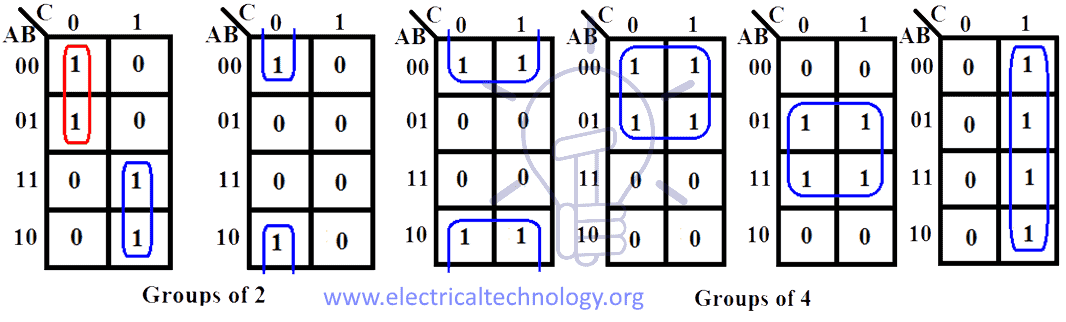
The beauty of the Karnaugh map lies in its ability to simplify complex Boolean expressions through visual inspection. The key principle is to identify groups of adjacent cells containing "1" values. These groups represent common terms within the Boolean function, and their identification leads to simplification.

Rules for Grouping:

• Adjacency: Cells are considered adjacent if they share a common side, even if they appear at opposite ends of a row or column.
• Size: Groups can be of any size, as long as they contain a power of 2 number of cells (1, 2, 4, 8, etc.).
• Maximize: Aim to form the largest possible groups, as this minimizes the number of terms in the final expression.
• Overlap: Groups can overlap, and cells can be part of multiple groups.

Deriving the Simplified Expression: A Practical Example

Let’s consider a Boolean function represented by the following truth table:

A	B	C	Output
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

Following the steps outlined above, we can construct a Karnaugh map for this function:

      C
    0  1
  +-------+
A|0 1| 1 0 |
B+-------+
  1| 0 1 | 1 1 |
  +-------+

By visually inspecting the map, we can identify the following groups:

• Group 1: A single cell containing a "1" in the top left corner (A=0, B=0, C=0).
• Group 2: A group of four cells containing "1" values in the top and bottom right corners (A=0, B=1, C=1; A=1, B=0, C=1; A=1, B=1, C=1; A=0, B=1, C=0).

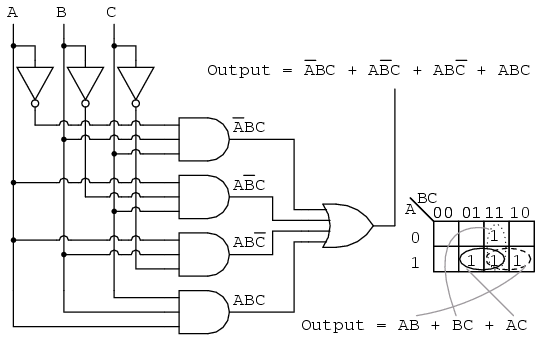
The simplified Boolean expression derived from these groups is:

Output = A’B’C’ + B’C + BC

This expression is significantly simpler than the original one obtained directly from the truth table, highlighting the power of Karnaugh maps for simplification.

Importance and Benefits of Karnaugh Maps

The use of Karnaugh maps offers significant advantages in digital logic design:

• Simplification: They facilitate the derivation of minimal Boolean expressions, leading to efficient hardware implementations.
• Visual Representation: The graphical nature of Karnaugh maps provides an intuitive understanding of the logical relationships within the function.
• Error Reduction: The visual representation helps identify errors in the initial Boolean expression or truth table.
• Improved Readability: Simplified expressions are easier to understand and debug, contributing to better design practices.
• Design Optimization: Minimized expressions lead to reduced gate count, lowering costs and improving performance.

FAQs about Karnaugh Maps for Three Variables

Q: What is the difference between a Karnaugh map and a truth table?

A: While both represent Boolean functions, a truth table provides a tabular representation of all input combinations and their corresponding output values. In contrast, a Karnaugh map offers a visual representation that facilitates the identification of groups and the derivation of simplified expressions.

Q: Can Karnaugh maps be used for functions with more than three variables?

A: Yes, but the complexity of the map increases with the number of variables. For four variables, a 2x4x2 grid is required, and the visualization becomes more challenging. For functions with more than four variables, alternative simplification methods, such as the Quine-McCluskey algorithm, are typically employed.

Q: How do I handle "don’t care" conditions in a Karnaugh map?

A: "Don’t care" conditions occur when the output value for a specific input combination is irrelevant. These conditions are represented by "X" in the Karnaugh map and can be used to create larger groups, further simplifying the expression.

Q: What are some common mistakes to avoid when using Karnaugh maps?

A:

• Incorrect Group Formation: Ensure that groups are formed correctly, adhering to the rules of adjacency and size.
• Missing Groups: Carefully examine the map to identify all possible groups, including those that might seem insignificant.
• Gray Code Misinterpretation: Double-check the order of variables and their values to ensure they follow the Gray code system.

Tips for Efficient Karnaugh Map Usage

• Start with a Truth Table: Begin by constructing a truth table to define the Boolean function.
• Organize the Variables: Use Gray code to arrange the variables in the map, ensuring that adjacent cells differ by only one variable.
• Identify the Largest Groups: Prioritize forming the largest possible groups to minimize the number of terms in the final expression.
• Don’t Forget Don’t Cares: Utilize "don’t care" conditions to create larger groups and further simplify the expression.
• Double-Check the Expression: Verify the simplified expression against the original truth table or function to ensure accuracy.

Conclusion: Empowering Digital Logic Design with Karnaugh Maps

Karnaugh maps are an invaluable tool for simplifying Boolean expressions, enabling efficient hardware implementation and design optimization. By understanding the principles of map construction, grouping, and simplification, engineers can effectively utilize this graphical method to reduce complex logic circuits, minimize cost, and improve overall system performance. As a fundamental technique in digital logic design, Karnaugh maps continue to play a vital role in the creation of modern electronic systems.

Closure

Thus, we hope this article has provided valuable insights into Mastering Logic with Karnaugh Maps: A Comprehensive Guide to 3-Variable Maps. We thank you for taking the time to read this article. See you in our next article!